Map概览
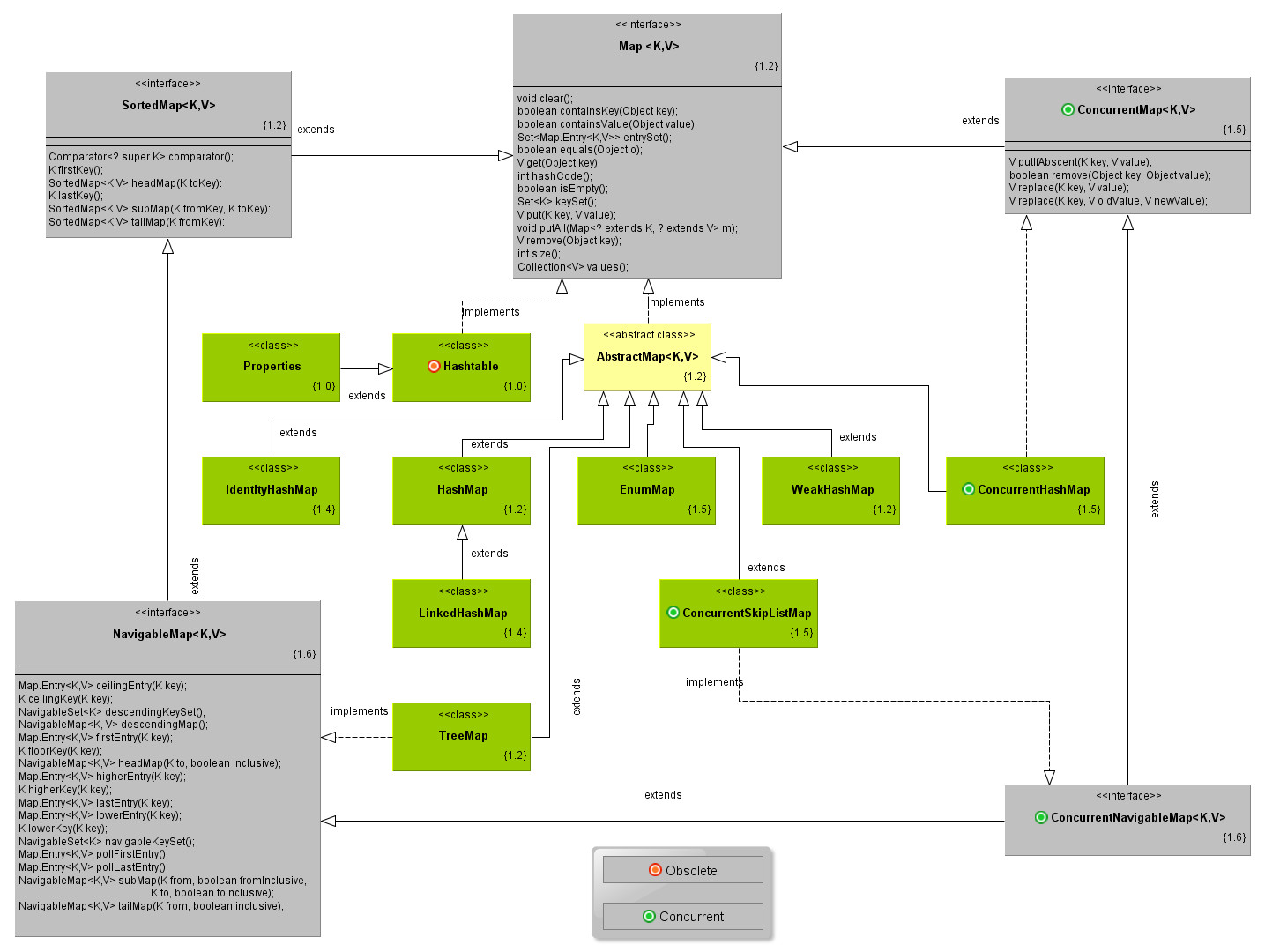
Map类型的数据结构重点在于一个名值对的集合体。它本身要保证里面有一个名字的键值作为元素的唯一识别,并关联对应的值。所以,如果我们去查看Map的的定义,里面会有很多关于键值和对应值的操作,比如说containsKey, containsValue,V get(Object key), V put(K key, V value)等方法。我们常用的HashTable, HashMap, TreeMap, ConcurrentHashMap都是对应Map接口的具体实现。
其中HashTable和HashMap是一种经典的哈希表实现,在很多面试的过程中也会讨论到这些问题。HashMap内部实现是使用一个数组,每个数组的元素又构成了一个链表结构。这可以说是教科书上定义的哈希表的一个经典实现。另外TreeMap的实现是使用了数据结构里面的红黑树,它可以保证里面所有的元素访问操作都是排序的,而且操作的时间复杂度都是在logN的级别。而对于ConcurrentHashMap来说,它内部是采用了分段,并对不同段采用独立的锁的机制进行设计,尽可能保证足够大的并行度。
Map接口
| 方法名 | 方法详细定义 | 说明 |
|---|---|---|
| containsKey | boolean containsKey(Object key); | 判断名是否存在 |
| containsValue | boolean containsValue(Object value); | 判断值是否存在 |
| get | V get(Object key); | 读取元素 |
| put | V put(K key, V value); | 设置元素 |
| keySet | Set |
所有key值合集 |
| values | Collection |
所有value的集合 |
| entrySet | Set<Map.Entry<K, V» entrySet(); | 键值对集合 |
HashMap
我们从书本上看到的hash表根据不同的需要可以有不同的实现方式,比如有的直接用线性表,有的用链表数组。在hash值的映射规则上也各不相同。在jdk的实现里,HashMap是采用链表数组形式的结构:

在JDK1.6中,HashMap采用的是位桶+链表的方式,即我们常说的散列链表的方式,而JDK1.8中采用的是位桶+链表/红黑树的方式,也是非线程安全的。当某个位桶的链表的长度达到某个阀值(8)的时候,这个链表就将转换成红黑树。使查询最差复杂度由O(N) 变成了 O(logN)
Entry结构
在HashMap内部,有一个transient Entry[] table;这样的结构数组,它保存所有Entry的一个列表。而Entry的定义是一个典型的链表结构,不过由于既要有Key也要有Value,所以包含了Key, Value两个值。他们的定义如下:
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
// 返回旧值
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
// 对象相同或者Key和value都相等
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
构造函数
在HashMap里面保存元素的table是可以动态增长的,它有一个默认的长度16,在HashMap的构造函数中,可以指定初始数组的长度。通过这个初始长度值,构造一个长度为2的若干次方的数组。
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
static final float DEFAULT_LOAD_FACTOR = 0.75f; // 初始的负载因子0.75,超出则rehash
//当add一个元素到某个位桶,其链表长度达到8时将链表转换为红黑树
static final int TREEIFY_THRESHOLD = 8;
//位桶的链表长度小于6时,解散红黑树
static final int UNTREEIFY_THRESHOLD = 6;
//默认的最小的扩容量64,为避免重新扩容冲突,至少为4 * TREEIFY_THRESHOLD=32,即默认初始容量的2倍
static final int MIN_TREEIFY_CAPACITY = 64;
transient Node<K,V>[] table;
transient Set<Map.Entry<K,V>> entrySet;
transient int size;
int threshold;
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
添加和扩容
put元素就是一个放置元素的过程,首先也是找到对应的索引,然后再把元素放到链表里面去。如果链表里有和元素相同的,则更新对应的value,否则就放到链表末尾。
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
static final int hash(Object key) {
int h;
// HashMap里是接受null类型的值作为key或者value的
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0) // 数组为空
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null) // 对应key的hash链表为空
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k)))) // 匹配到链表头
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) { //遍历链表
if ((e = p.next) == null) { // 遍历到末尾没发现,则添在末尾
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // 对应的key存在节点
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold) // 不存在对应的key,先判断扩容
resize();
afterNodeInsertion(evict);
return null;
}
Hash值的求法,由于使用了红黑树来处理大的链表开销,所以hash这边可以更加省力了,只用计算hashCode并移动到低位就可以了。Hash的目的是让HashCode更均匀,真正的在数组中的index是hash % (table.length-1)
static final int hash(Object key) {
int h;
// //计算hashCode,并无符号移动到低位
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
int index = hash & (tab.length - 1);
调整数组长度的时候,由于HashMap本身的独特性质,它需要重新做一次映射。因为新数组的长度不一样了,再映射的时候要对链表里面所有的元素(整个链表hash值还是相同的)根据新的长度进行重新映射来对应到不同的位置。
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length; //旧容量
int oldThr = threshold; //旧阈值
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) { //已经足够大了,不能再增大
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY) // 翻一翻(两倍扩容)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // 本来数组为空,初始化数组容量和阈值
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); // 扩容阈值是通过容量和负载因子的乘积决定的,当数组容量超过扩容阈值时,调用resize,rehash
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; //新数组,准备rehash
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) { //遍历老数组
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null) // 只有链表表头有数据
newTab[e.hash & (newCap - 1)] = e; // 将e放在新位置
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do { //旧链表遍历,
next = e.next;
//注意此处为oldCap而不是(oldCap-1),即hash小于原先数组大小的存入loHead变量
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else { // hash大于原先数组大小的存入hiHead变量
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) { //hash小于原先数组大小,则在新数组位置还是j
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) { //hash大于原先数组大小,在新数组中位置为(oldCap + j)
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
get方法
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//hash & (length-1)得到对象的保存位
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
//如果第一个节点是TreeNode,说明采用的是数组+红黑树结构处理冲突
//遍历红黑树,得到节点值
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
// 遍历链表
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
它这里就是一个映射,查找的过程。找到映射的点之后再和链表里的元素逐个比较,保证找到目标值。因为是hash表,会存在多个值映射到同一个index里面,所以这里还要和链表里的元素做对比。
HashTable
HashTable在java.util包下面,继承自Dictionary抽象类。实现了同步的HashTable也是上图一样的数组链表的结构,它的同步使用锁来保证的,并且所有同步操作使用的是同一个锁对象。这样若有n个线程同时在get时,这n个线程要串行的等待来获取锁。
构造函数,与HashMap不同的是,HashTable默认的table长度是11
private transient Entry<?,?>[] table;
private transient int count;
private int threshold;
private float loadFactor;
public Hashtable() {
this(11, 0.75f);
}
public Hashtable(int initialCapacity) {
this(initialCapacity, 0.75f);
}
添加元素时,如果HashTable要调整长度,通过rehash方法,将长度设置为原有长度x2 + 1。新增的链表节点添加在表头,与JDK1.8的HashMap实现不同。对于HashTable的实现,如果我们要往里面添加null元素则会抛出异常。
public synchronized V put(K key, V value) {
// Value不可以为null
if (value == null) {
throw new NullPointerException();
}
// Makes sure the key is not already in the hashtable.
Entry<?,?> tab[] = table;
int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length; //数组中的index
@SuppressWarnings("unchecked")
Entry<K,V> entry = (Entry<K,V>)tab[index];
for(; entry != null ; entry = entry.next) {
if ((entry.hash == hash) && entry.key.equals(key)) {
V old = entry.value;
entry.value = value;
return old;
}
}
addEntry(hash, key, value, index);
return null;
}
private void addEntry(int hash, K key, V value, int index) {
modCount++;
Entry<?,?> tab[] = table;
if (count >= threshold) {
// Rehash the table if the threshold is exceeded
rehash();
tab = table;
hash = key.hashCode();
index = (hash & 0x7FFFFFFF) % tab.length;
}
// Creates the new entry.
@SuppressWarnings("unchecked")
Entry<K,V> e = (Entry<K,V>) tab[index];
tab[index] = new Entry<>(hash, key, value, e); // 将新增的entry添加在表头
count++;
}
protected void rehash() {
int oldCapacity = table.length;
Entry<?,?>[] oldMap = table;
// overflow-conscious code
int newCapacity = (oldCapacity << 1) + 1; // 旧长度翻翻加一
if (newCapacity - MAX_ARRAY_SIZE > 0) {
if (oldCapacity == MAX_ARRAY_SIZE)
// Keep running with MAX_ARRAY_SIZE buckets
return;
newCapacity = MAX_ARRAY_SIZE;
}
Entry<?,?>[] newMap = new Entry<?,?>[newCapacity];
modCount++;
threshold = (int)Math.min(newCapacity * loadFactor, MAX_ARRAY_SIZE + 1);
table = newMap;
for (int i = oldCapacity ; i-- > 0 ;) {
for (Entry<K,V> old = (Entry<K,V>)oldMap[i] ; old != null ; ) {
Entry<K,V> e = old;
old = old.next;
int index = (e.hash & 0x7FFFFFFF) % newCapacity;
e.next = (Entry<K,V>)newMap[index];
newMap[index] = e;
}
}
}
方法的线程安全:
看到前面贴出来的一部分实例代码,我们会看到HashTable里的方法带了synchronized的修饰。而HashMap里却没有。没错,对于HashTable来说,它是线程安全的。而对于HashMap来说却不是。不过如果在多线程的情况下,我们需要考虑性能或者数据访问一致性的话,HashMap就不是一个合理的选择,我们更应该考虑一下ConcurrentHashMap。
get方法
public synchronized V get(Object key) {
Entry<?,?> tab[] = table;
int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length;
for (Entry<?,?> e = tab[index] ; e != null ; e = e.next) {
if ((e.hash == hash) && e.key.equals(key)) {
return (V)e.value;
}
}
return null;
}
这里HashMap里面的迭代器是标准的Iterator接口实现,而HashTable里的则不一样,它采用的是Enumerator,这个类实现了Enumeration和Iterator两个接口,这部分的关键定义如下:
private <T> Enumeration<T> getEnumeration(int type) {
if (count == 0) {
return Collections.emptyEnumeration();
} else {
return new Enumerator<>(type, false);
}
}
private <T> Iterator<T> getIterator(int type) {
if (count == 0) {
return Collections.emptyIterator();
} else {
return new Enumerator<>(type, true);
}
}
为什么这部分要分别定义呢?因为原有的Enumeration接口是比较老的版本里的定义,它和Iterator接口的定义不一样。为了保证后面版本的jdk里也可以采用标准迭代器的方式来访问HashTable里的元素同时也为了和原来使用它的老代码兼容,这里就同时实现了两个接口。而他们两个接口里定义的东西基本上是一样的,除了Iterator接口里还定义了一个remove()方法。
ConcurrentHashMap jdk1.6版本
ConcurrentHashMap是Java5中新增加的一个线程安全的Map集合,可以用来替代HashTable。对于ConcurrentHashMap是如何提高其效率的,可能大多人只是知道它使用了多个锁代替HashTable中的单个锁,也就是锁分离技术(Lock Stripping)。实际上,ConcurrentHashMap对提高并发方面的优化,还有一些其它的技巧在里面(比如你是否知道在get操作的时候,它是否也使用了锁来保护?)。
Entry定义:
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
volatile V val;
volatile Node<K,V> next;
}
从代码中可以看到,这里是一个很典型的链表的节点。和前面的HashMap有点不同的地方在于,这里的value和next都采用了volatile的修饰。这样保证在有多个线程访问的情况下不会出现数据不一致性。
分段结构
ConcurrentHashMap中对这个数据结构,针对并发稍微做了一点调整。 它把区间按照并发级别(concurrentLevel),分成了若干个segment。默认情况下内部按并发级别为16来创建。对于每个segment的容量,默认情况也是16。当然并发级别(concurrentLevel)和每个段(segment)的初始容量都是可以通过构造函数设定的。
创建好默认的ConcurrentHashMap之后,它的结构大致如下图:

static class Segment<K,V> extends ReentrantLock implements Serializable {
private static final long serialVersionUID = 2249069246763182397L;
final float loadFactor;
Segment(float lf) { this.loadFactor = lf; }
}
Segment继承了ReentrantLock,表明每个segment都可以当做一个锁。(ReentrantLock前文已经提到,不了解的话就把当做synchronized的替代者吧)这样对每个segment中的数据需要同步操作的话都是使用每个segment容器对象自身的锁来实现。只有对全局需要改变时锁定的是所有的segment。
分拆锁和分离锁:
分拆锁(lock spliting)就是若原先的程序中多处逻辑都采用同一个锁,但各个逻辑之间又相互独立,就可以拆(Spliting)为使用多个锁,每个锁守护不同的逻辑。
分拆锁有时候可以被扩展,分成可大可小加锁块的集合,并且它们归属于相互独立的对象,这样的情况就是分离锁(lock striping)。(摘自《Java并发编程实践》)
get方法
public V get(Object key) {
int hash = hash(key); // throws NullPointerException if key null
return segmentFor(hash).get(key, hash);
}
它没有使用同步控制,交给segment去找,再看Segment中的get方法:
V get(Object key, int hash) {
if (count != 0) { // read-volatile
HashEntry e = getFirst(hash);
while (e != null) {
if (e.hash == hash && key.equals(e.key)) {
V v = e.value;
if (v != null)
return v;
return readValueUnderLock(e); // recheck
}
e = e.next;
}
}
return null;
}
V readValueUnderLock(HashEntry e) {
lock();
try {
return e.value;
} finally {
unlock();
}
}
get操作不需要锁。第一步是访问count变量,这是一个volatile变量,由于所有的修改操作在进行结构修改时都会在最后一步写count变量,通过这种机制保证get操作能够得到几乎最新的结构更新。对于非结构更新,也就是结点值的改变,由于HashEntry的value变量是volatile的,也能保证读取到最新的值。接下来就是对hash链进行遍历找到要获取的结点,如果没有找到,直接访回null。对hash链进行遍历不需要加锁的原因在于链指针next是final的。但是头指针却不是final的,这是通过getFirst(hash)方法返回,也就是存在table数组中的值。这使得getFirst(hash)可能返回过时的头结点,例如,当执行get方法时,刚执行完getFirst(hash)之后,另一个线程执行了删除操作并更新头结点,这就导致get方法中返回的头结点不是最新的。这是可以允许,通过对count变量的协调机制,get能读取到几乎最新的数据,虽然可能不是最新的。要得到最新的数据,只有采用完全的同步。
put方法
put操作一上来就锁定了整个segment,这当然是为了并发的安全,修改数据是不能并发进行的,必须得有个判断是否超限的语句以确保容量不足时能够rehash,而比较难懂的是这句int index = hash & (tab.length - 1),原来segment里面才是真正的hashtable,即每个segment是一个传统意义上的hashtable,如上图,从两者的结构就可以看出区别,这里就是找出需要的entry在table的哪一个位置,之后得到的entry就是这个链的第一个节点,如果e!=null,说明找到了,这是就要替换节点的值(onlyIfAbsent == false),否则,我们需要new一个entry,它的后继是first,而让tab[index]指向它,什么意思呢?实际上就是将这个新entry插入到链头,剩下的就非常容易理解了。
V put(K key, int hash, V value, boolean onlyIfAbsent) {
lock();
try {
int c = count;
if (c++ > threshold) // ensure capacity
rehash();
HashEntry[] tab = table;
int index = hash & (tab.length - 1);
HashEntry first = (HashEntry) tab[index];
HashEntry e = first;
while (e != null && (e.hash != hash || !key.equals(e.key)))
e = e.next;
V oldValue;
if (e != null) {
oldValue = e.value;
if (!onlyIfAbsent)
e.value = value;
}
else {
oldValue = null;
++modCount;
tab[index] = new HashEntry(key, hash, first, value);
count = c; // write-volatile
}
return oldValue;
} finally {
unlock();
}
}
ConcurrentHashMap jdk1.8版本
关于1.6版本的 ConcurrentHashMap,网上的资料一大把,主要也就是采用锁分段技术,相比 HashTab 的每个方法都是同步方法,每个操作都需要锁整个链表数组,效率确实要好很多 查看1.6版本的 ConcurrentHashMap 中 Segment 的实现,该 Segment 继承自 ReentrantLock,而且对于所有的写操作都需要先获取锁,读操作不需要锁,除非读到的值为 null,才会继续获取锁重读一次。1.6 Segment#put 操作,每次 put/replace 需要先锁对应的 Segment,而 get 操作者不需要
1.8 版本的 ConcurrentHashMap 不再采用 Segment 实现,而是改用 Node,Node 是一个链表的结构,每个节点可以引用到下一个节点
transient volatile Node<K,V>[] table;
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
volatile V val;
volatile Node<K,V> next;
}
对应的 put 操作也不再使用 ReentrantLock 使用,而是采用 CAS + 同步的方式实现 1)整个 Map 第一次 put 的时候,map 中用于存放数据的 Node[] 还是null,注意,1.8版本的 ConcurrentHashMap 在构造函数中不会初始化 Node 数组,而是第一次 put 操作的时候初始化; 2)根据对应的key hash 到具体的索引,如果该索引对应的 Node 为 null,则采用 CAS 操作更新整个 table 3)如果该key hash 对应的 Node 不为 null,则在该 Node 对象上采用同步方式更新 Node 链表最尾部元素的值,可以看到1.8版本中的 ConcurrentHashMap 在 put 操作的时候同步操作也只是在对应的一个 node 节点上同步,而不需要在整个 table 上同步,而至于为什么1.8采用 synchronized 关键字而不是采用 ReentrantLock 方式实现同步,也许是因为1.8版本的虚拟机对 synchronized 关键字已经有足够的优化吧
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
synchronized (f) { // !!!!注意这里的synchronized关键字
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f;; ++binCount) {
K ek;
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
Node<K,V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
else if (f instanceof TreeBin) {
Node<K,V> p;
binCount = 2;
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
addCount(1L, binCount);
return null;
}
ConcurrentHashMap完全可以代替HashTable的说法,如果你的环境要求“强一致性”的话,就不能用ConcurrentHashMap了,它的get,clear方法和迭代器都是“弱一致性”的。不过真正需要“强一致性”的场景可能非常少,我们大多应用中ConcurrentHashMap是满足的。
TreeMap
TreeMap和TreeSet算是java集合类里面比较有难度的数据结构。和普通的HashMap不一样,普通的HashMap元素存取的时间复杂度一般是O(1)的范围。而TreeMap内部对元素的操作复杂度为O(logn)。虽然在元素的存取方面TreeMap并不占优,但是它内部的元素都是排序的,当需要查找某些元素以及顺序输出元素的时候它能够带来比较理想的结果。可以说,TreeMap是一个内部元素排序版的HashMap。这里会对TreeMap内部的具体实现机制和它所基于的红黑树做一个详细的介绍。
其实在HashMap和ConcurrentHashMap中,在链表数据量大(超过8)的情况下都有采用红黑树(TreeBin)的结构,提高查找效率。
红黑树(Red-Black Tree)
红黑树本质上是一棵一定程度上相对平衡的二叉搜索树。为什么这么说呢?我们从前面讨论二叉搜索树的文章中可以看到。一棵二叉搜索树理想情况下的搜索和其他元素操作的时间复杂度是O(logn)。但是,这是基于一个前提,即二叉搜索树本身构造出来的树是平衡的。如果我们按照普通的插入一个元素就按照二叉树对应关系去摆的话,在一些极端的情况下会失去平衡。比如说我们通过插入一个顺序递增或者递减的一组元素,那么最后的结构就相当于一个双向链表。对其中元素的访问也不可能达到O(logn)这样的级别。
平衡:左右子树高度差不超过1
所以,在这样的情况下,我们就希望有那么一种机制或者数据结构能够保证我们既能构造出一棵二叉搜索树来,而且它天生就是平衡的。这样就有了红黑树。当然,为了同时达到这两个目标,红黑树设定了一些特定的属性限制,也使得它本身的实现比较复杂。我们在下面的定义中就可以看到。
红黑树的官方定义如下:
红黑树是一种二叉树,同时它还满足下列5个特性:
- 每个节点是红色或者黑色的。
- 根节点是黑色的。
- 每个叶节点是黑色的。(这里将叶节点的左右空子节点作为一个特殊的节点对待,设定他们必须是黑色的。)
- 如果一个节点是红色的,则它的左右子节点都必须是黑色的。
- 对任意一个节点来说,从它到叶节点的所有路径必须包含相同数目的黑色节点。
这部分的定义看得让人有点不知所云,我们先看一个红黑树的示例:

假定其中带阴影的节点为红色节点,则上图为一棵红黑树。假定我们取根节点来考察,它到任意一个叶节点要走过3个黑色的节点。这样,从任意一个节点到叶节点只需要经历过的黑色节点相同就可以了,可以说这是一个放松了的平衡衡量标准。
节点定义
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
}

添加元素
添加元素的过程可以大致的分为两个步骤。和二叉搜索树类似,我们添加元素也是需要通过比较元素的值,找到添加元素的地方。这部分基本上没有什么变化。第二步则是一个调整的过程。因为红黑树不一样,当我们添加一个新的元素之后可能会破坏它固有的属性。主要在于两个地方,一个是要保证新加入元素后,到所有叶节点的黑色节点还是一样的。另外也要保证红色节点的子节点为黑色节点。
还有一个就是,结合TreeMap的map特性,我们添加元素的时候也可能会出现新加入的元素key已经在数中间存在了,那么这个时候就不是新加入元素,而是要更新原有元素的值。
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
上述的代码看起来比较多,不过实际上并不复杂。第3到9行主要是判断在根节点为null的情况下,我们的put方法相当于直接创建一个节点并关联到根节点。后面的两个大的if else块是用来判断是否设定了comparator的情况下的比较和加入元素操作。对于一些普通的数据类型,他们默认实现了Comparable接口,所以我们用compareTo方法来比较他们。而对于一些自定义实现的类,他们的比较关系在一些特殊情况下需要实现Comparator接口,这就是为什么前面要针对这两个部分要进行区分。在这两个大的块里面主要做的就是找到要添加元素的地方,如果有相同key的情况,则直接替换原来的value。
第42行及后面的部分需要处理添加元素的情况。如果在前面的循环块里面没有找到对应的Key值,则说明已经找到了需要插入元素的位置,这里则要在这个地方加入进去。添加了元素之后,基本上整个过程就结束了。
这里有一个方法fixAfterInsertion(),在我们前面的讨论中提到过。每次当我们插入一个元素的时候,我们添加的元素会带有一个颜色,而这个颜色不管是红色或者黑色都可能会破坏红黑树定义的属性。所以,这里需要通过一个判断调整的过程来保证添加了元素后整棵树还是符合要求的。这部分的过程比较复杂,我们拆开来详细的一点点讲。
在看fixAfterInsertion的实现之前,我们先看一下树的左旋和右旋操作。这个东西在fixAfterInsertion里面用的非常多。
旋转
树的左旋和右旋的过程用一个图来表示比较简单直观:

从图中可以看到,我们的左旋和右旋主要是通过交换两个节点的位置,同时将一个节点的子节点转变为另外一个节点的子节点。具体以左旋为例,在旋转前,x是y的父节点。旋转之后,y成为x的父节点,同时y的左子节点成为x的右子节点。x原来的父节点成为后面y的父节点。这么一通折腾过程就成为左旋了。同理,我们也可以得到右旋的过程。
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
调整过程
我们知道,在红黑树里面,如果加入一个黑色节点,则导致所有经过这个节点的路径黑色节点数量增加1,这样就肯定破坏了红黑树中到所有叶节点经过的黑色节点数量一样的约定。所以,我们最简单的办法是先设置加入的节点是红色的。这样就不会破坏这一条约定。但是,这样的调整也会带来另外一个问题,如果我这个要加入的节点它的父节点已经是红色的了呢?这岂不是又破坏了原来的约定吗?是的,在这种情况下,我们就要通过一系列的调整来保证最终它成为一棵合格的红黑树。但是这样比我们加入一个黑色节点然后去调整相对来说范围要狭窄一些。现在我们来看看怎么个调整法
场景1: N节点的父节点P以及P的兄弟节点都是红色,而它的祖父节点G为黑色

在这种情况下,只要将它的父节点P以及节点U设置为黑色,而祖父节点G设置为红色。这样就保证了任何通过G到下面的叶节点经历的黑色节点还是和原来一样,为1.而且也保证了红色节点的子节点不为红色。这种场景的一个前提是只要保证要添加的节点和它的父节点以及父节点的兄弟节点都是红色,则通过同样的手法进行转换。这和加入的节点是父节点的左右子节点无关。
场景2: N节点的父节点P是红色,但是它的祖父节点G和它父节点的兄弟节点U为黑色。
这种情形实际上还取决于要插入的元素N的位置,如果它是P的右子节点,则先做一个左旋操作,转换成右边的情形。这样,新加入的节点保证成为父节点的左子节点。

在上图做了这么一种转换之后,我们还需要做下一步的调整,如下图:

这一步是通过将P和G的这一段右旋,这样G则成为了P的右子节点。然后再将P的颜色变成黑色,G的颜色变成红色。这样就保证新的这一部分子树还是包含相同的黑色子节点。
前面我们对这两种情况的讨论主要涵盖了这么一种大情况,就是假设我们新加入节点N,它的父节点P是祖父节点G的左子节点。在这么一个大前提下,我们再来想想前面的这几种场景是否已经足够完备。我们知道,这里需要调整的情况必然是新加入的节点N和父节点P出现相同颜色也就是红色的情况。那么,在他们同时是红色而且父节点P是祖父节点G的左子节点的情况下,P的兄弟节点只有两种可能,要么为红色,要么为黑色。这两种情况正好就是我们前面讨论的图所涵盖的。
如果父节点P作为祖父节点G的右子节点,则情况和作为左子节点的情况对称。我们可以按照类似的方法来处理。
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x))); // 取当前节点的叔父节点
if (colorOf(y) == RED) { //叔父节点也为红色,则满足第一种情况: 将父节点和叔父节点设置为黑色,祖父节点为红色。
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) { // 第二种情况中,节点是父节点的右子节点,所以先左旋一下
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK); // 第二种情况,父节点和祖父节点做一个右旋操作,然后父节点变成黑色,祖父节点变成红色
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
前面代码中while循环的条件则是判断当前节点是否有父节点,而且父节点的颜色和它是否同样为红色。我们默认加入的元素都设置成红色。我在代码里把父节点是祖父节点左孩子的情况做了注释。另外一种情况也可以依葫芦画瓢的来分析。
删除元素
删除元素的过程和普通二叉搜索树的搜索过程大体也比较类似,首先是根据待删除节点的情况进行分析:
1, 待删除节点没有子节点, 则直接删除该节点。如下图:

2, 待删除节点有一个子节点,则用该子节点替换它的父节点:

3, 待删除节点有两个子节点,则取它的后继节点替换它,并删除这个后继节点原来的位置。它可能有两种情况:


这几种情况就是二叉搜索树里面删除元素的过程。这里就不再赘述。我们主要看红黑树有些不一样的地方。下面是删除方法实现的主要代码:
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
第7到12行代码就是判断和处理待删除节点如果有两个子节点的情况。通过找到它的后继节点,然后将后继节点的值覆盖当前节点。这一步骤完成之后,后续的就主要是将原来那个后继节点删除。第15行及以后的代码主要就是处理删除这个节点的事情。当然,考虑到红黑树的特性,这里有两个判断当前待删除节点是否为黑色的地方。我们知道,如果当前待删除节点是红色的,它被删除之后对当前树的特性不会造成任何破坏影响。而如果被删除的节点是黑色的,这就需要进行进一步的调整来保证后续的树结构满足要求。这也就是为什么里面需要调用fixAfterDeletion这个方法。
删除后的调整
删除元素之后的调整和前面的插入元素调整的过程比起来更复杂。它不是一个简单的在原来过程中取反。我们先从一个最基本的点开始入手。首先一个,我们要进行调整的这个点肯定是因为我们要删除的这个点破坏了红黑树的本质特性。而如果我们删除的这个点是红色的,则它肯定不会破坏里面的属性。因为从前面删除的过程来看,我们这个要删除的点是已经在濒临叶节点的附近了,它要么有一个子节点,要么就是一个叶节点。如果它是红色的,删除了,从上面的节点到叶节点所经历的黑色节点没有变化。所以,这里的一个前置条件就是待删除的节点是黑色的。
在前面的那个前提下,我们要调整红黑树的目的就是要保证,这个原来是黑色的节点被删除后,我们要通过一定的变化,使得他们仍然是合法的红黑树。我们都知道,在一个黑色节点被删除后,从上面的节点到它所在的叶节点路径所经历的黑色节点就少了一个。我们需要做一些调整,使得它少的这个在后面某个地方能够补上。
ok,有了这一部分的理解,我们再来看调整节点的几种情况。
\1. 当前节点和它的父节点是黑色的,而它的兄弟节点是红色的:

这种情况下既然它的兄弟节点是红色的,从红黑树的属性来看,它的兄弟节点必然有两个黑色的子节点。这里就通过节点x的父节点左旋,然后父节点B颜色变成红色,而原来的兄弟节点D变成黑色。这样我们就将树转变成第二种情形中的某一种情况。在做后续变化前,这棵树这么的变化还是保持着原来的平衡。
\2. 1) 当前节点的父节点为红色,而它的兄弟节点,包括兄弟节点的所有子节点都是黑色。

在这种情况下,我们将它的兄弟节点设置为红色,然后x节点指向它的父节点。这里有个比较难以理解的地方,就是为什么我这么一变之后它就平衡了呢?因为我们假定A节点是要调整的节点一路调整过来的。因为原来那个要调整的节点为黑色,它一旦被删除就路径上的黑色节点少了1.所以这里A所在的路径都是黑色节点少1.这里将A的兄弟节点变成红色后,从它的父节点到下面的所有路径就都统一少了1.保证最后又都平衡了。
当然,大家还会有一个担忧,就是当前调整的毕竟只是一棵树中间的字数,这里头的节点B可能还有父节点,这么一直往上到根节点。你这么一棵字数少了一个黑色节点,要保证整理合格还是不够的。这里在代码里有了一个保证。假设这里B已经是红色的了。那么代码里那个循环块就跳出来了,最后的部分还是会对B节点,也就是x所指向的这个节点置成黑色。这样保证前面亏的那一个黑色节点就补回来了。
2) 当前节点的父节点为黑色,而它的兄弟节点,包括兄弟节点的所有子节点都是黑色。
这种情况和前面比较类似。如果接着前面的讨论来,在做了那个将兄弟节点置成红色的操作之后,从父节点B开始的所有子节点都少了1.那么这里从代码中间看的话,由于x指向了父节点,仍然是黑色。则这个时候以父节点B作为基准的子树下面都少了黑节点1. 我们就接着以这么一种情况向上面推进。
\3. 当前节点的父节点为红色,而它的兄弟节点是黑色,同时兄弟节点有一个节点是红色。

这里所做的操作就是先将兄弟节点做一个右旋操作,转变成第4种情况。当然,前面的前提是B为红色,在B为黑色的情况下也可以同样的处理。
\4. 在当前兄弟节点的右子节点是红色的情况下。

这里是一种比较理想的处理情况,我们将父节点做一个左旋操作,同时将父节点B变成黑色,而将原来的兄弟节点D变成红色,并将D的右子节点变成黑色。这样保证了新的子树中间根节点到各叶子节点的路径依然是平衡的。大家看到这里也许会觉得有点奇怪,为什么这一步调整结束后就直接x = T.root了呢?也就是说我们一走完这个就可以把x直接跳到根节点,其他的都不需要看了。这是因为我们前面的一个前提,A节点向上所在的路径都是黑色节点少了一个的,这里我们以调整之后相当于给它增加了一个黑色节点,同时对其他子树的节点没有任何变化。相当于我内部已经给它补偿上来了。所以后续就不需要再往上去调整。
前面讨论的这4种情况是在当前节点是父节点的左子节点的条件下进行的。如果当前节点是父节点的右子节点,则可以对应的做对称的操作处理,过程也是一样的。
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
LinkedHashMap
LinkedHashMap是HashMap的一个子类,它保留插入的顺序,如果需要输出的顺序和输入时的相同,那么就选用LinkedHashMap。 LinkedHashMap是Map接口的哈希表和链接列表实现,具有可预知的迭代顺序。此实现提供所有可选的映射操作,并允许使用null值和null键。此类不保证映射的顺序,特别是它不保证该顺序恒久不变。
默认是按插入顺序排序,如果指定按访问顺序排序,那么调用get方法后,会将这次访问的元素移至链表尾部,不断访问可以形成按访问顺序排序的链表。 可以重写removeEldestEntry方法返回true值指定插入元素时移除最老的元素。

public class LinkedHashMap<K, V> extends HashMap<K, V> implements Map<K, V>
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
transient LinkedHashMap.Entry<K,V> head;
transient LinkedHashMap.Entry<K,V> tail;
final boolean accessOrder; //排序模式,访问顺序 true; 插入顺序 false
WeakHashMap
和HashMap一样,WeakHashMap 也是一个散列表,它存储的内容也是键值对(key-value)映射,而且键和值都可以是null。
不过WeakHashMap的键是“弱键”。在 WeakHashMap 中,当某个键不再正常使用时,会被从WeakHashMap中被自动移除。更精确地说,对于一个给定的键,其映射的存在并不阻止垃圾回收器对该键的丢弃,这就使该键成为可终止的,被终止,然后被回收。某个键被终止时,它对应的键值对也就从映射中有效地移除了。
强引用:平时我们编程的时候例如:Object object=new Object();那object就是一个强引用了。如果一个对象具有强引用,那就类似于必不可少的生活用品,垃圾回收器绝不会回收它。当内存空 间不足,Java虚拟机宁愿抛出OutOfMemoryError错误,使程序异常终止,也不会靠随意回收具有强引用的对象来解决内存不足问题。 软引用(SoftReference):如果一个对象只具有软引用,那就类似于可有可物的生活用品。如果内存空间足够,垃圾回收器就不会回收它,如果内存 空间不足了,就会回收这些对象的内存。只要垃圾回收器没有回收它,该对象就可以被程序使用。软引用可用来实现内存敏感的高速缓存。 软引用可以和一个引用队列(ReferenceQueue)联合使用,如果软引用所引用的对象被垃圾回收,Java虚拟机就会把这个软引用加入到与之关联 的引用队列中。 弱引用(WeakReference):如果一个对象只具有弱引用,那就类似于可有可物的生活用品。弱引用与软引用的区别在于:只具有弱引用的对象拥有更 短暂的生命周期。在垃圾回收器线程扫描它 所管辖的内存区域的过程中,一旦发现了只具有弱引用的对象,不管当前内存空间足够与否,都会回收它的内存。不过,由于垃圾回收器是一个优先级很低的线程, 因此不一定会很快发现那些只具有弱引用的对象。 弱引用可以和一个引用队列(ReferenceQueue)联合使用,如果弱引用所引用的对象被垃圾回收,Java虚拟机就会把这个弱引用加入到与之关联 的引用队列中。 虚引用(PhantomReference):“虚引用”顾名思义,就是形同虚设,与其他几种引用都不同,虚引用并不会决定对象的生命周期。如果一个对象 仅持有虚引用,那么它就和没有任何引用一样,在任何时候都可能被垃圾回收。 虚引用主要用来跟踪对象被垃圾回收的活动。虚引用与软引用和弱引用的一个区别在于:虚引用必须和引用队列 (ReferenceQueue)联合使用。当垃圾回收器准备回收一个对象时,如果发现它还有虚引用,就会在回收对象的内存之前,把这个虚引用加入到与之 关联的引用队列中。程序可以通过判断引用队列中是否已经加入了虚引用,来了解被引用的对象是否将要被垃圾回收。程序如果发现某个虚引用已经被加入到引用队 列,那么就可以在所引用的对象的内存被回收之前采取必要的行动。
WeakHashMap维护了一个ReferenceQueue,保存了所有存在引用的Key对象。
private final ReferenceQueue<K> queue = new ReferenceQueue<K>();
WeakHashMap.Entry< K,V >中并没有保存Key,只是将Key与ReferenceQueue关联上了。
private static class Entry<K,V> extends WeakReference<K> implements Map.Entry<K,V> {
private V value;
private final int hash;
private Entry<K,V> next;
Entry(K key, V value, ReferenceQueue<K> queue, int hash, Entry<K,V> next) {
super(key, queue);
this.value = value;
this.hash = hash;
this.next = next;
}
……
}
WeakHashMap中有一个私有的expungeStaleEntries()方法,会在大部分共有方法中被调用。这个方法会将ReferenceQueue中所有失效的引用从Map中去除。
注意: WeakHashMap的Key是弱引用,Value不是。 WeakHashMap不会自动释放失效的弱引用,仅当包含了expungeStaleEntries()的共有方法被调用的时候才会释放。
ConcurrentSkipListMap
ConcurrentSkipListMap优点:
-
ConcurrentSkipListMap 的key是有序的。
-
ConcurrentSkipListMap 支持更高的并发。ConcurrentSkipListMap 的存取时间是log(N),和线程数几乎无关。也就是说在数据量一定的情况下,并发的线程越多,ConcurrentSkipListMap越能体现出他的优势。
-
在非多线程的情况下,应当尽量使用TreeMap。此外对于并发性相对较低的并行程序可以使用Collections.synchronizedSortedMap将TreeMap进行包装,也可以提供较好的效率。对于高并发程序,应当使用ConcurrentSkipListMap,能够提供更高的并发度。所以在多线程程序中,如果需要对Map的键值进行排序时,请尽量使用ConcurrentSkipListMap,可能得到更好的并发度
什么是SkipList
Skip list(跳表)是一种可以代替平衡树的数据结构,默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中,以0-1随机数决定一个数据的向上攀升与否,通过“空间来换取时间”的一个算法,在每个节点中增加了向前的指针,在插入、删除、查找时可以忽略一些不可能涉及到的结点,从而提高了效率。
Skip list比较简单,实现起来会比较容易,虽然和平衡树有着相同的时间复杂度(O(logn)),但是skip list的常数项会相对小很多。Skip list在空间上也比较节省。一个节点平均只需要1.333个指针(甚至更少)。

Skip list结构图(以7,14,21,32,37,71,85序列为例)
Skip list的性质 (1) 由很多层结构组成,level是通过一定的概率随机产生的。 (2) 每一层都是一个有序的链表,默认是升序,也可以根据创建映射时所提供的Comparator进行排序,具体取决于使用的构造方法。 (3) 最底层(Level 1)的链表包含所有元素。 (4) 如果一个元素出现在Level i 的链表中,则它在Level i 之下的链表也都会出现。 (5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
ConcurrentSkipListMap
ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList(跳表)结构实现,在理论上能够在O(log(n))时间内完成查找、插入、删除操作。
链表中查找“32”节点

需要4步(红色部分表示路径)
跳表中查找“32”节点

忽略索引垂直线路上路径的情况下,只需要2步(红色部分表示路径)。
下面说说Java中ConcurrentSkipListMap的数据结构。 (01) ConcurrentSkipListMap继承于AbstractMap类,也就意味着它是一个哈希表。 (02) Index是ConcurrentSkipListMap的内部类,它与“跳表中的索引相对应”。HeadIndex继承于Index,ConcurrentSkipListMap中含有一个HeadIndex的对象head,head是“跳表的表头”。 (03) Index是跳表中的索引,它包含“右索引的指针(right)”,“下索引的指针(down)”和“哈希表节点node”。node是Node的对象,Node也是ConcurrentSkipListMap中的内部类。
doPut() 的作用就是将键值对添加到“跳表”中,主干部分“对应的精简后的doPut()的代码”如下(仅供参考):
private V doPut(K kkey, V value, boolean onlyIfAbsent) {
Comparable<? super K> key = comparable(kkey);
for (;;) {
// 找到key的前继节点
Node<K,V> b = findPredecessor(key);
// 设置n为key的后继节点
Node<K,V> n = b.next;
for (;;) {
// 新建节点(对应是“要被插入的键值对”)
Node<K,V> z = new Node<K,V>(kkey, value, n);
// 设置“b的后继节点”为z
b.casNext(n, z);
// 随机获取一个level
// 然后在“第1层”到“第level层”的链表中都插入新建节点
int level = randomLevel();
if (level > 0)
insertIndex(z, level);
return null;
}
}
}
remove()是通过doRemove()将ConcurrentSkipListMap中的key对应的键值对删除的, 主干部分“对应的精简后的doRemove()的代码”如下
final V doRemove(Object okey, Object value) {
Comparable<? super K> key = comparable(okey);
for (;;) {
// 找到“key的前继节点”
Node<K,V> b = findPredecessor(key);
// 设置n为“b的后继节点”(即若key存在于“跳表中”,n就是key对应的节点)
Node<K,V> n = b.next;
for (;;) {
// f是“当前节点n的后继节点”
Node<K,V> f = n.next;
// 设置“当前节点n”的值为null
n.casValue(v, null);
// 设置“b的后继节点”为f
b.casNext(n, f);
// 清除“跳表”中每一层的key节点
findPredecessor(key);
// 如果“表头的右索引为空”,则将“跳表的层次”-1。
if (head.right == null)
tryReduceLevel();
return (V)v;
}
}
}
doGet()是通过findNode()找到并返回节点的
private Node<K,V> findNode(Comparable<? super K> key) {
for (;;) {
// 找到key的前继节点
Node<K,V> b = findPredecessor(key);
// 设置n为“b的后继节点”(即若key存在于“跳表中”,n就是key对应的节点)
Node<K,V> n = b.next;
for (;;) {
// 如果“n为null”,则跳转中不存在key对应的节点,直接返回null。
if (n == null)
return null;
Node<K,V> f = n.next;
// 如果两次读取到的“b的后继节点”不同(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (n != b.next) // inconsistent read
break;
Object v = n.value;
// 如果“当前节点n的值”变为null(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (v == null) { // n is deleted
n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // b is deleted
break;
// 若n是当前节点,则返回n。
int c = key.compareTo(n.key);
if (c == 0)
return n;
// 若“节点n的key”小于“key”,则说明跳表中不存在key对应的节点,返回null
if (c < 0)
return null;
// 若“节点n的key”大于“key”,则更新b和n,继续查找。
b = n;
n = f;
}
}
}
java concurrency: ConcurrentHashMap
浅析jdk1.6和1.8版本的ConcurrentHashMap